Charles Petzold

Whenever we visit Deirdre's mother and sister in Utica (such as last Saturday) we always pay a visit to nearby Berry Hill Book Shop in Deansboro. It's literally a barn with three levels, and they purport to carry 85,000 used books.

It was there in the mathematics section where I found F. Emerson Andrews' little book New Numbers: How Acceptance of a Duodecimal Base Would Simplify Mathematics (Essential Books, 1944) with a dust jacket for just $1 more than its original price of $2.50.

After I got the book home and did a little research, I discovered that it's kind of famous in its own little way.

In 1934 and 1935 Andrews wrote two articles for the Atlantic Monthly discussing the advantages of a base-12 number system. (The first of these articles can be found on the Web site of the Dozenal Society of America, which carries on Andrews' work.) These were expanded into a book entitled New Numbers in 1935. This was the first book-length treatise on base-12 published in America, and apparently only the second published in English. (The first was Dozens versus Tens, or The Ounce, the Inch, and the Penny considered as standards of Weight, Measure, and Money, and with Reference to a Duodecimal Notation by Thomas Leech, published in London in 1866.) The 1944 second edition of New Numbers (the one I bought) made some corrections and changed some of the nomenclature.

Of course, programmers like myself are likely to exclaim "Base twelve?! What a dork! Everybody knows that the human race should really switch to base sixteen to be consistent with our glorious digital computers." But we would be wrong. People shouldn't have to adjust their number system (or their handwriting or anything else) to the computer; the computer should adjust to us.

Of course, we're all dorks if we think that the human race will actually convert to a number system other than decimal. Even Andrews seems to know this will never happen. Although he puts forth a good case for base-12, he says:

This is not, however, a crusading attempt. It know far too well the leech-clutch of habit to suppose that any present change is probably; perhaps it is not even desirable. This is more nearly an invitation to gallant adventure. Let the reader follow who will, casting tradition to the winds and picking a new trail which cuts across centuries of habit and mountain ranges of established thought. (p. 15)

Historically, the whole problem came about because counting preceded mathematics, and people used their fingers to count. But nobody selecting a number base for ease in doing common arithmetic would ever choose ten. Ten is equally divisible by only 2 and 5. Very often in daily life, we must divide quantities by 3 or 4, and that's where base-12 excels because twelve is divisible by 2, 3, 4, and 6.

What would a base-12 system look like? To the digits 0 through 9, Andrews adds two more. For the digit that corresponds to decimal ten, he nominates the dek, which is the same as the Roman numeral for ten: X. For the digit that corresponds to eleven he proposes the el, which looks like this: Ɛ. To avoid confusion, he displays all duodecimal numbers in italics, a convention I will also use in this blog entry. To avoid further confusion, the duodecimal number 10 he calls do, short for dozen and pronounced "dough" (although persons of the post-Simpsons era would find it hard not pronouncing it "do'h"). Apprently in the first edition of the book, this number was called a zen (see p. 62). The number 100 is a gro, because it's equal to 144 in decimal, or a gross.

(By the way, the symbol for the el, in Andrews' words, "is not an epsilon, but a 'fancy' form of the italic E known to printers as 'swash E'" (p. 147) I couldn't find anything called a "swash E" in the Unicode character set, so I'm using a capital epsilon, character code 0x0190, and the Lucida sans Unicode font, so it may show up as a box or something if you don't have that font installed.)

The single most significant benefit we get from base-12 is this:

The fraction 1/3 is 0.4

but many other simple fractions are also cleaner in duodecimal:

1/12 == 0.1
1/9 == 0.14
1/8 == 0.16
1/6 == 0.2
1/4 == 0.3
1/2 == 0.6
2/3 == 0.8
3/4 == 0.9

As you've undoubtedly experienced, when you divide 1 in half and then continue dividing the result in half, the decimals grow by one digit with each operation: 0.5, 0.25, 0.125, 0.0625, 0.03125, and so forth. With duodecimal, the progression is a lot cleaner: 0.6, 0.3, 0.16, 0.09, 0.046, 0.023, and so forth.

How do you determine if a decimal integer is equally divisible by 3? Well, there's a trick: You add up all the digits and if that's divisible by 3 then the original number is divisible by three. How can you determine if a duodecimal integer is equally divisible by 3? If the number ends in 0, 3, 6, or 9. A duodecimal number is divisible by 6 if the number ends in 0 or 6.

How can you determine if a decimal integer is equally divisible by 4? It's another trick. If the last two digits are divisible by 4, so is the original number. But a duodecimal number is equally divisible by 4 if the number ends in 0, 4, or 8.

New Numbers included a handy multiplication table on a card tucked into a sleeve on the inside back cover and, astonishingly, the card was still there in the copy I bought:

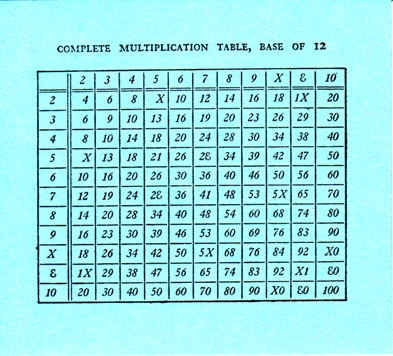
As you can see, a number of nice patterns show up here that would probably facilitate the memorization of the multiplication table.

One accidental result of base-12 that I thought interesting is that 1.5 is a very good approximation to the square root of 2.

Of course, the metric system just compounds all the problems that exist with decimal in the first place, and that's been long recognized. What's one-third of a yard? One foot. What's one-third of a foot? Four inches. What's one-third of a meter? It's 3 decimeters plus 3 centimeters plus 3 millimeters plus... Early in New Numbers, Andrews even quotes Napoleon on this issue:

Twelve has always been preferred to ten as a divisor.... The new system is all based on the meter and conveys no idea to my mind. I can understand the twelfth part of an inch, but not the thousandth part of a meter.... La Place himself assured me that if all the objections I had made to it had been pointed out to him before its adoption, he would have recognized its defects and given it up. (p. 38, apparently from "5 pp. in History of France under Napoleon, by C. T. de Montholon.")

New Numbers is a fun and persuasive book, but I think that any serious attempt to introduce duodecimal into common life would require that it coexist with decimal for several centuries. To avoid confusion in written numbers, the duodecimal system would require new symbols for all the digits except 0, and coming up with entirely new but simple symbols would probably be the biggest challenge of all.