Charles Petzold

With two-dimensional graphics, it's usually fairly easy to specify the coordinates that govern the location and size of a graphical figure. With 3D graphics, you might not have this convenience: Often you're working with primitives that have a fixed location and size, and you must use transforms to move and resize the figures.

In Chapter 2 of my new book 3D Programming for Windows I show how to use TranslateTransform3D and ScaleTransform3D to assemble simple figures from unit cubes. (A unit cube has a width, height, and depth of 1 unit and is centered on the origin of the 3D coordinate system.) In Chapter 3 I continue those demonstrations with rotation, and Chapter 7 has some more advanced math behind deriving complex rotations in 3D space.

I'd like to show another demonstration here using unit cubes to construct a fairly simple figure (a 7-pointed star) in 3D space. Fortunately all the trigonometry involved will be in two dimensions on the XY plane.

Here's a seven-pointed star with a radius of 1 centered on the origin of a conventional 2D Cartesian coordinate system. Each point of the start is associated with an angle measured counter-clockwise from the positive X axis:

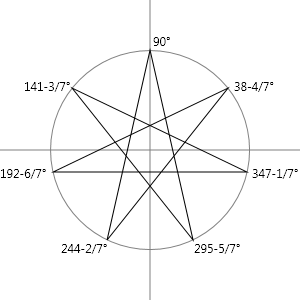
I started with 90° at the top and then just incremented by 51-3/7° (360 ÷ 7) going counter-clockwise. Each of the points of the star is also associated with a coordinate point whose X value is the cosine of the angle and whose Y value is the sine:

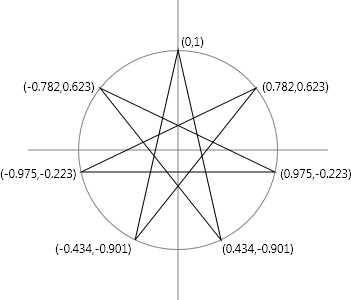
The seven lines that form the star are the same lengths, which can be calculated using the Pythagorean theorem. Here's the calculation of the length of the line from the upper-right of the star to the bottom-left.

((–0.434 – 0.782)² + (–0.901 – 0.623)²)^0.5 = 1.950

I'm going to build the seven-pointed star from unit cubes, and the first step is to turn a unit cube into a "plank" that is 1.95 units long, (let's say) 1 unit deep, and (let's say also) 0.05 units thick. Here's the XAML file that performs this very first step:

SevenPointedStarStep1.xaml

The unit cube is defined as a resource, and a GeometryModel3D based on this cube is also defined as a resource. This GeometryModel3D resource has a ScaleTransform3D applied with a ScaleX factor of 1.95 and a ScaleY of 0.05. The resource is named "plank" and Step 1 creates just one ModelVisual3D based on this resource. The figure is still centered on the origin:

The objective now is to create seven figures based on this resource, and apply translation and rotation transforms to them so they form the seven legs of the star. By default, rotations occur around the origin, so in this case it's easier to rotate the plank first and then translate it to its proper location. As an example, let's look at the leg from the upper-right point (0.782, 0.623) to the lower-left point (–0.434, –0.901). The angle this leg makes with the X axis can be calculated as the inverse tangent of the ratio of the difference between the Y and X coordinates:

tan^-1((0.623 + 0.901) / (0.782 + 0.434)) = tan^-1(1.524 / 1.216) = 51.4°

The center of the plank at the origin must be translated to the mid-point of that leg, which is the average of the points at the ends, or:

((0.782 – 0.434) / 2, (0.623 – 0.901) / 2) = (0.174, –0.139)

The plank can thus be positioned with an AxisAngleRotation3D element with an Axis property of (0, 0, 1) and an Angle of 51.4, followed by a TranslateTransform3D with OffsetX and OffsetY properties of 0.174 and –0.139, respectively.

Continue with the other legs. Of course, you can take advantage of symmetry to reduce the calculations. Here's the resultant XAML file:

SevenPointedStarStep2.xaml

And it looks like this:

Of course, once you have a figure like this completed, it's always fun to animate it, if only to verify that the sides actually change shade as they make different angles with the light source. Here's a version that rotates the star around the Z axis:

SevenPointedStarStep3.xaml

And then I thought: Wouldn't it be fun to animate the seven planks so they started in a kind of stack and then moved to their proper positions in the star? Each of the TranslateTransform3D and AxisAngleRotation3D elements would need to have x:Name attributes, and I'd need another 13 DoubleAnimation elements. (It's not 14 because one of the legs has no rotation.) But the animations would be fairly simple because they'd have only simple From attributes and no To attributes. So here it is:

SevenPointedStar.xaml

	Buy my book and we'll both be happy!
	Amazon.com	BookSense.com	quantumbooks
	Barnes & Noble	Amazon Canada	Amazon UK
	Amazon Français	Amazon Deutsch	Amazon Japan