Charles Petzold

A couple years ago a friend of mine got a New York City Teaching Fellowship to teach in the public schools here. The subject she chose to teach was mathematics because, as she said, "In math there's only one correct answer."

That statement came to mind while I was sitting in deep contemplation pondering a package of Charmin, a product that Procter & Gamble discreetly refers to as "bathroom tissue" but which in our genteel household goes by the name papier de twa-lay, as in "Hey, who left one square of papier de twa-lay on the roll?"

Charmin comes in four distinct roll sizes, called Regular, Big, Giant, and Mega. No, these sizes do not accomodate four different sizes of bums. The Big roll has twice as many sheets as the Regular, the Giant has 2.5 times as many sheets as Regular, and Mega has four times as many, as shown on this convenient chart:

The Mega roll is so big that it generally requires an adapter to fit in the typical puny papier de twa-lay dispenser.

Each sheet on the roll, we are informed, is 10.8 cm (4.27") wide — that's the width of the roll itself — and 10.1 cm (4") long. So, the Regular roll is a total of 176 × 4" long, or 58-2/3 feet. From there you can easily determine the lengths of the other four sizes: 117-1/3 feet, 146-2/3 feet, and 234-2/3 feet.

These numbers refer to the total length of the roll as it might appear when draped over a tree branch on Hallowe'en. But that's the trivial calculation. If you're the type of person who gazes off distractedly and thinks "I wonder what the relationships are between the radii of these four sizes" then you just might be a mathematician.

This particular problem has an easy solution and a hard solution, and neither approach involves anything so crass as actually measuring the things with a ruler. Even the hard way involves a simplification, but it all turns out to be OK in the end.

I'll be using subscripts R, B, G, and M to refer to the Regular, Big, Giant and Mega sizes. The relationships between the Length of each roll is available from the chart:

L_R = length of Regular roll
L_B = 2 × L_R
L_G = 2.5 × L_R
L_M = 4 × L_R

Let's give ourselves the freedom to refer to L_i where i can be R, B, G, or M. Let's define F_i as the multiplicative Factor of the lengths relative to L_R. Hence,

F_i = L_i / L_R

For i equal to R, B, G, and M, F_i equals 1, 2, 2.5, and 4, respectively.

Let's also define variables for the radii:

R_R = radius of Regular roll
R_B = radius of Big roll
R_G = radius of Giant roll
R_M = radius of Mega roll
R_T = radius of paper tube

We can also refer to R_i where i equals R, B, G, and M (but not T). We're basically interested in finding R_i as a function of R_R, R_T, and F_i.

A couple other symbols will be useful:

W = width of roll (4.27")
P = thickness of paper

Of course, we have to assume that the paper on the four sizes of rolls is wound around the paper tube consistently and uniformly among the roll sizes. The Volume of the paper based on the Length, Width, and Paper thickness can be calculated like so:

V_i = L_i × W × P

Because each size roll has the same Width and Paper thickness, the Volume is obviously proportional to the Length or,

V_i = F_i × V_R

The Volume occupied by the paper can also be calculated as the volume of a cylinder, which is the area of the cross section of the cylinder (πR²) times the Width of the roll. It's complicated a bit because the volume occupied by the paper tube must be excluded:

V_i = WπR_i² – WπR_T²

For the Regular roll, the volume is:

V_R = WπR_R² – WπR_T²

These two equations can be hooked together using the relationship between the two volumes shown above:

WπR_i² – WπR_T² = F_i × (WπR_R² – WπR_T²)

All the W terms drop out because we really could have performed this exercise by just examining the cross section. The π's drop out as well:

R_i² – R_T² = F_i × (R_R² – R_T²)

So,

R_i² = F_i × R_R² – F_i × R_T² + R_T²

And here's the final result that gives us the desired relationship:

R_i = (F_i × R_R² – (F_i – 1) × R_T²)^½

Anyone who cares to measure the radius of the paper tube and the Regular roll can plug the numbers in and determine the radii for the larger rolls. For example, if R_T (the radius of the paper tube) is 0.75" and R_R (the radius of the Regular roll) is 2" (and I'm pretty much making up these numbers because I'm not going to measure them) then the radius of the Big roll would be 2.72".

The more difficult approach to this problem is to treat the roll of paper as a series of concentric circles of paper:

The paper on the roll is actually a spiral, but obviously these concentric circles are a good approximation. Each size of Charmin is associated with a characteristic number N_i (where i equals R, B, G, or M) that indicates the number of concentric circles of paper in the roll.

These concentric circles of paper always have a thickness of P with an inner side and an outer side. The inside of the innermost circle of paper is at radius R_T, the radius of the tube. The outer side is at radius R_T + P. The average is the radius R_T + P/2. The next circle of paper has an average radius of R_T + 3P/2, and so forth. In general, for circle n (where n ranges from 1 to N_i), the radius is R_T + (2n-1)P/2. Thus, each of these circles of paper has a circumference equal to:

C_n = 2π × (R_T + (2n-1)P / 2) for n = 1 to N_i

The entire length of the paper on the roll is equal to the summation of these circumferences (and forgive the slight change in appearance as I switch to bitmaps of an MS Word document created using the Equation Editor):

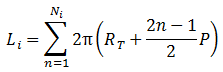
This doesn't look like it's going to come anywhere close to the original result, but let's move on anyway. We can pull some constant stuff outside the summations and break the summations down:

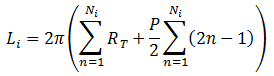
And then we can reduce it even further to leave just one summation:

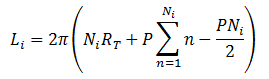
The sum 1 + 2 + 3 + ... + K is always equal to (K)(K + 1) / 2, so:

L_i = PπN_i² + 2πR_TN_i

We need to get rid of the N_i term if there's any hope of making this method match up with the first one. Fortunately, it's possible to calculate R_i knowing the characteristic number N_i. Just multiply it by the thickness of paper P and add R_T:

R_i = N_i × P + R_T

From that, solve for N_i:

N_i = (R_i - R_T) / P

Now substitute that into the formula for L_i:

L_i = Pπ((R_i – R_T) / P)² + 2πR_T((R_i – R_T) / P)

This is just getting worse and worse, but let's expand that square in the first expression and also expand the second expression:

L_i = Pπ((R_i² – 2R_iR_T + R_T²) / P²) + 2π((R_iR_T – R_T²) / P)

Fortunately, stuff starts falling out, until you're left with:

L_i = (π / P) × (R_i² – R_T²)

For the Regular roll,

L_R = (π / P) × (R_R² – R_T²)

Since

L_i = F_i × L_R

then

R_i² – R_T² = F_i × (R_R² – R_T²)

which is exactly one of the intermediate results I got in the earlier derivation.

It's math: There's only one right answer, and the two methods are equivalent.