Canonical Splines in WPF and Silverlight
January 22, 2009
New York, N.Y.
Windows Forms has two methods named DrawCurve and DrawClosedCurve that draw canonical (aka cardinal) splines. Like the more familiar Bézier spline, the canonical spline is a cubic polynomial; however unlike the Bézier, the canonical spline passes through each of its control points, and the amount of curvature is governed by a tension parameter.
A complete derivation of the cubic polynomials for the canonical spline can be found in my Windows Forms books Programming Microsoft Windows with C#, pages 645-646, and Programming Microsoft Windows with Microsoft Visual Basic .NET, pages 638-639, but here's the simple version:
If four consective control points are pt0, pt1, pt2, and pt3, then the canonical spline curve between pt1 and pt2 has a slope at pt1 equal to the product of the tension and the slope of the straight line between pt0 and pt2. (If pt0 is not available, which happens in the first segment of an unclosed curve, then pt1 is used instead for that slope calculation.) The slope of the curve at pt2 is equal to the tension times the slope of the straight line between pt1 and pt3, or between pt1 and pt2 if pt3 is not available. This information, together with two vital pieces of information in the first paragraph of this blog entry, is actually all you need to derive the cubic parametric formulas for the canonical spline.
What's most peculiar about the canonical spline is that each segment is based not only on the start point and end point of the segment (in my example, pt1 and pt2) but also on the neighboring points (pt0 and pt2). I don't know why the canonical spline didn't become part of the Windows Presentation Foundation or Silverlight, but I have a hunch that the problem is related to this peculiarity: Proper integration of the canonical spline in WPF and Silverlight would require PathSegment derivatives named something like CanonicalSplineSegment and PolyCanonicalSplineSegment. But these classes would have a very different behavior from the other PathSegment derivatives because they would require access to neighboring points outside the actual segment. Perhaps there was just no good way to do this.
At any rate, if you just need to use a canonical spline by itself, I've created WPF and Silverlight classes named CanonicalSpline that help you out. (The WPF version is derived from Shape; the Silverlight version is derived from — I'll give you one guess — UserControl.) Here's a demo of the Silverlight version:
I've provided a scrollbar that lets you set the tension to a value between –10 and 10. The default value is 0.5; if you set it to 0, the curve degenerates into straight lines. At values greater than 1, the curve begins exhibiting excessive curviness; at negative values, the curve takes roundabout paths between each pair of points. At a value of –9, you'll get the display shown on page 642 of the C# WinForms book (634 of the VB version):
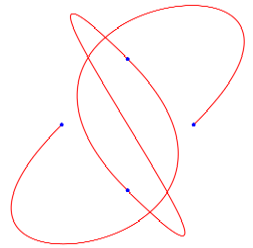
You can also drag the actual control points around, and add new control points or remove points. A checkbox lets you close the spline. Notice that closing the spline results in a new segment being drawn from the last point to the first point, but it also affects the previous first and last segments, because these are now influenced by the last and first control points, respectively.
You can also fill the interior (notice how filling doesn't require closing the spline) and choose between the EvenOdd and Nonzero fill rules. The easiest way to see the difference is to arrange five points in a star:
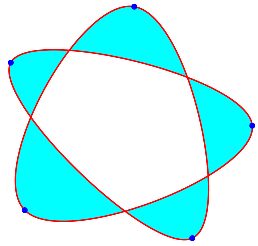
The EvenOdd fill rule leaves the center "pentagon" uncolored. The Nonzero rule colors it.
I like to set up several points, close the curve, fill it with the EvenOdd rule, and then move the scrollbar back and forth. It keeps me entertained for minutes.
This demo program doesn't show one of the features of the canonical spline code I've created here: You can actually specify different tension values for each control point. This alters the parametric equations for the canonical spline somewhat: For each segment of the spline, two tension values are required, one associated with pt1 and the other with pt2. The first tension value is multiplied by the straight-line slope from pt0 to pt2 and the second is multiplied by the straight-line slope from pt1 to pt3.
This feature is obviously helpful for fine-tuning the image. For example, suppose you had a collection of 5 points like so:
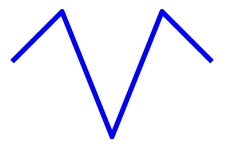
You use the CanonicalSpline class to draw these points setting the Tension property to 1:
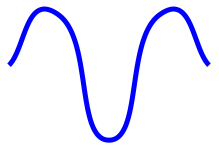
Well, this is not quite what you want. You want the top parts to be rounded, but you want the center point unrounded, and you want the curve at the end-points to be a little straighter. The solution is to set the Tensions property (notice the plural) to a DoubleCollection that consists of the values 0, 1, 0, 1, 0. The result looks like this:
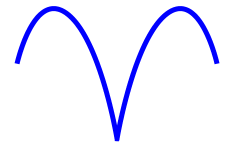
All three of those images were produced by the following WPF XAML file:
-
<Page xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"
xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
xmlns:spline="clr-namespace:CanonicalSplineLib;assembly=CanonicalSplineLib">
<Page.Resources>
<Style TargetType="spline:CanonicalSpline">
<Setter Property="Points"
Value="100 75 150 25 200 150 250 25 300 75" />
<Setter Property="Stroke" Value="Blue" />
<Setter Property="StrokeThickness" Value="5" />
</Style>
</Page.Resources>
<StackPanel>
<spline:CanonicalSpline Tension="0" />
<spline:CanonicalSpline Tension="1" />
<spline:CanonicalSpline Tensions="0 1 0 1 0" />
</StackPanel>
</Page>
Let's look at the Visual Studio CanonicalSplineDemo solution containing both the WPF and Silverlight code. I tried to share as much code as possible. There are five projects:
-
CanonicalSplineDemo and CanonicalSplineDemo.Web comprise the Silverlight application.
-
CanonicalSplineDemo.Wpf is the WPF application.
-
CanonicalSplineLib is the Silverlight DLL.
-
CanonicalSplineLib.Wpf is the WPF DLL.
In Visual Studio, you can select the "Set as StartupProject" menu option on either the CanonicalSplineDemo.Web or CanonicalSplineDemo.Wpf project.
For convenience in sharing code, both DLL's have the same namespace name and assembly name, CanonicalSplineLib. The two DLLs share a file (and static internal class) named CanonicalSplineHelper. This class contains the code to generate a PathGeometry from a set of control points and other information.
The WPF DLL also contains a public class named CanonicalSpline that derives from Shape and defines the additional seven properties (all backed with dependency properties):
-
Points of type PointCollection: The control points. The collection must contain at least two unique points or nothing will be drawn.
-
Tension of type double.
-
Tensions of type DoubleCollection. This property provides the point-specific tension values unless the collection is null or empty, in which case Tension is used for all points. Tension is always used if the Points collection contains only two points. Customarily, the Tensions collection will be the same size as the Points collection, but if it is smaller, then it's looped. For example, if Tensions contains three values, 0, 2, 1, and there are seven control points in the Points collection, then these seven points are associated with tension values of 0, 2, 1, 0, 2, 1, 0.
-
IsClosed of type bool. This property governs whether an additional segment is drawn from the last point to the first, and is also used to set the same-named property in the PathFigure of the PathGeometry generated to represent the spline.
-
IsFilled of type bool. This property is used to set the same-named property in the PathFigure of the PathGeometry generated to represent the spline. This property affects hit-testing and clipping of the path.
-
FillRule of type FillRule. This property is used to set the same-named property in the PathGeometry object and determines how interior areas are filled.
-
Tolerance of type double governs the accuracy of the polyline approximation to the spline. Each line segment of the polyline approximation has an (extremely) approximate length of Tolerance device-independent units (of 1/96th inch). The default value is 0.25, indicating that each line segment is roughly 1/400th inch in length.
The Silverlight DLL also has a public class named CanonicalSpline but which derives from UserControl. This class defines all the same properties defined by the WPF version of CanonicalSpline plus all the properties defined by Shape (Fill, Stretch, Stroke, StrokeDashArray, StrokeDashCap, StrokeDashOffset, StrokeEndLineCap, StrokeLineJoin, StrokeMiterLimit, StrokeStartLineCap, and StrokeThickness).
For the Silverlight application (which you can run from the link above) I created a small UserControl derivative named Dot to represent the points, and another UserControl derivative named MainPage that displays the spline and all the controls that let you fiddle around with it.
The WPF application has a Window class derivative named MainWindow but the content is just the MainPage class that it shares with the Silverlight version.