Non-Affine Transforms in Silverlight
January 30, 2009
Utica, N.Y.
If you're an enthusiast of the Microsoft Office clip-art library, you may be familiar with this little fellow

who, I'm afraid, bears an uncanny resemblance to myself.
Just to have some fun with him, I wrote a little hack that converted his native format (WMF, or Windows Metafile Format) to something a bit easier to play around with in modern environments (XAML). The conversion resulted in a bunch of Polygon elements (16.2K worth) with their Fill and Points properties set.
The next step was a Silverlight program that displayed these polygons with some draggable blue dots attached to three of the four corners:
The Polygon elements defining the image reside in a Canvas, whose RenderTransform property is set to a MatrixTransform object. By dragging the three corners, you can effectively apply an affine matrix transform to the points, resulting in translation, scaling, rotation, or skewing, perhaps like this:
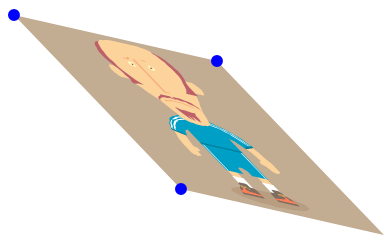
The only really tricky part of the program is the code that creates the matrix from the locations of the three dots, whose names indicate their locations, Upper-Left, Upper-Right, and Lower-Left:
-
double offsetX = dotUL.Center.X;
double offsetY = dotUL.Center.Y;
double m11 = (dotUR.Center.X - offsetX) / 192;
double m12 = (dotUR.Center.Y - offsetY) / 192;
double m21 = (dotLL.Center.X - offsetX) / 192;
double m22 = (dotLL.Center.Y - offsetY) / 192;
xform.Matrix = new Matrix(m11, m12, m21, m22, offsetX, offsetY);
The hard-coded values of 192 are the width and height of the image.
Because Silverlight (like WPF) allows only two-dimensional affine transforms, it is not possible to transform a rectangle into anything other than a parallelogram. That's why it's only possible to drag three corners: The fourth corner always goes along for the ride. The program displays the resultant matrix in the upper-right corner; the third column always contains the values 0, 0, 1, which indicates a 2D affine transform.
Here's the AffineTransformDemo source code. As usual, the only files I really messed with are Page.xaml and Page.xaml.cs, and the project includes a Dot class for the draggable dots.
Although Silverlight doesn't allow non-affine transforms, here's a Silverlight program that lets you interactively apply a non-affine transform to the figure:
You can independently drag any of the four corners and produce images that look like this:

It's a magic trick! Well, not really. The program is simply applying a non-affine transform to the polygon points before turning them over to Silverlight for rendering.
Here's the NonAffineTransformDemo source code. You'll discover a structure named MatrixNA ("matrix non-affine") that has a 9-argument constructor and 9 read-only properties named M11, M12, M13, M21, M22, M23, M31, M32, and M33. The structure overrides the multiplication operator and contains a Transform method that applies the transform to a Point.
You'll also discover a UserControl derivative named NonAffinePolygonTransformer with two properties: Matrix (of type MatrixNA?) and Polygons (of type List<Polygon>). The Polygons collection is set to the original Polygon elements that define the image. Whenever the Matrix or Polygons element changes, the NonAffinePolygonTransformer object loops through the original Polygon elements, creates new Polygon elements (if necessary), and copies the points from the original Polygon elements to the new Polygon elements, applying the Transform method of the MatrixNA to each Point. These new Polygon elements become children of a Canvas set as the element's Content property.
The Page.xaml.cs file contains the math to create the MatrixNA object based on the locations of the four dragged dots. It's basically the same math I discussed in my blog entry Non-Affine Transforms in 2D?, which uses WPF 3D to simulate non-affine transforms of bitmaps.
A little experimentation with NonAffineTransformDemo will reveal that you can pull the corners into any quadrilateral, but only if the quadrilateral is convex will the non-affine transform be correct. Otherwise, stuff in the interior of the image pops outside. While this might be amusing, it's not usually desired, and a real program would probably want to restrict mouse movement so the destination quadrilaterial is always convex.
I originally wanted to define the Polygons property in the NonAffinePolygonTransformer class to be of type PresentationFrameworkCollection<Polygon>. This class seems to play a role in Silverlight similar to the FreezableCollection<T> class in WPF, in that it provides change notifications if items in the collection change. Although PresentationFrameworkCollection<T> is widely used in Silverlight, it has no public constructor and is apparently entirely off-limits to Silverlight application programmer peons like myself.
I instead made the property of type List<Polygon>, and I created an instance of this collection in the NonAffinePolygonTransform constructor, but obviously my class doesn't receive a change notification when the collection is actually filled, which meant that the class didn't display an initial set of transformed polygons. I had to "fix" this problem by making the Matrix property of type MatrixNA? rather than MatrixNA, so that the Matrix property would fire a property-change notification when the property is initially set to a non-null value from Page.xaml.cs.