Charles Petzold

If books are like children (and many authors think of them in that way), then 3D Programming for Windows: Three-Dimensional Graphics Programming for the Windows Presentation Foundation is like the brilliant child so full of promise who gets mowed down by a drunk driver on the way to prom.

I thought every programmer alive would be excited about creating 3D animated graphics in XAML. Apparently that was not the case. The book has some wonderful stuff in it — I am still convinced that my discussion of quaternions is the best chapter-length tutorial on the subject in the English language — but sales of the book quickly died after about 4,000 copies. I kept some hope alive for awhile that some kind of tipping point might be reached when programmers would suddenly be scrambling to learn WPF 3D, but that no longer seems likely. So every time I go back to do some WPF 3D programming, I feel a little despondent about the tragedy of that book.

I received an email from someone working with WPF 3D who wanted to know how to draw arcs on the surface of a globe between two locations. Here's a 3D globe:

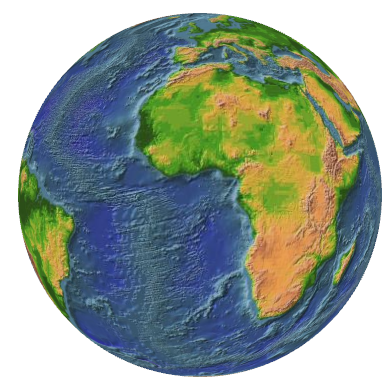
The code to generate the triangle mesh for this sphere is discussed in Chapter 6 of 3D Programming for Windows. Basically, the code generates a point in 3D space based on longitude and latitude values on the surface of the sphere. The longitude values in the code are a little different from conventional geographic longitudes, however. The longitudes in the code begin at 0° in the rear of the sphere (when viewed from the positive Z axis) and go to 360° in an eastward direction.

The sphere is covered by a bitmap I found on the web site of the Jet Propulsion Laboratory. That bitmap begins and ends at the International Date Line, so when it's wrapped around the sphere, the seam is at my internal longitude angles of 0° and 360° in negative Z space. When viewed head-on from positive Z space, the Prime Meridian is in front. Obviously my internal longitude angles are a little different from conventional longitude angles, but that doesn't matter.

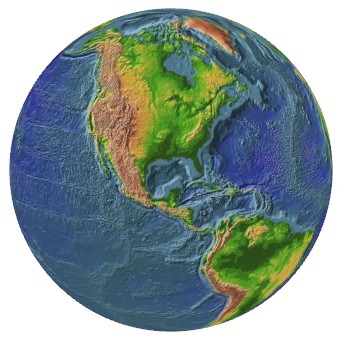
When viewed from the negative X axis and raising the camera into positive Y space, we get a better view of the U.S.:

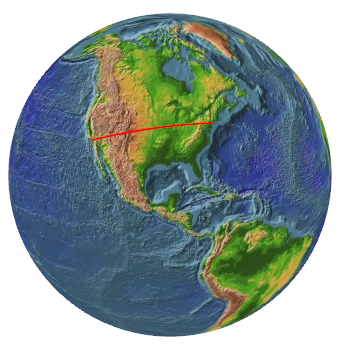
The email I received today asked about drawing arcs from one location to another. On the surface of a sphere, the shortest distance between two points follows the circumference of a great circle, which is a 2D circle in 3D space that shares a center and a radius with the sphere. The equator is a great circle; lines of longitude are great circles; but lines of latitude are not great circles (except for the equator).

As I was researching this problem and trying to figure out the best way to find this circle with the minimum amount of math, I encountered the following statement on the "Great Circle" article on Wofram's MathWorld site: "the geodesic giving the shortest path between two points on the surface of the equation lies on a plane that passes through the two points in question and also through center of the sphere."

This suggested to me that I could find points on the great circle connecting two locations in Cartesian space rather than spherical space. For each location, the geographic longitude and latitude would be converted to a 3D Cartesian point (x, y, z). These two points and the center of the sphere define a plane on which the great circle lies. Points calculated by linear interpolations between these two end-points are also on the surface of this plane. A line from the center of the sphere to these interpolated points is also on the surface of this plane. This line also defines a vector from the center of the sphere to the point. If the vector is normalized and then multiplied by the radius of the sphere, and then added to the center point (which is conveniently the origin) then the resultant points are on the circumference of the great circle.

These interpolated points lose their equidistance as they are projected to the surface of the sphere, but I wasn't worried about that. I used the points to construct a little band. Here's the arc between New York City and Los Angeles:

Here's the source code.

And please buy a book.