Charles Petzold: Five Ways to Incite Revolution

Five Ways to Incite Revolution

July 8, 2012
Roscoe, N.Y.

Suppose you want to start a revolution, and by that I mean, suppose you want to write a Windows 8 program to make an object revolve around the center of the screen, much like the Earth revolves around the Sun but without the cosmic implications.

I want to show you five different ways to do it, some less orthodox than others. In each case a "ball" 48 pixels in diameter revolves around the center of the screen with a orbital radius of 350 pixels.

The XAML file for the Revolution No. 1 program puts an Ellipse in a Canvas, but shrinks down the Canvas so that the Ellipse is positioned smack dab in the center of the page:

The code-behind file then installs a handler for the CompositionTarget.Rendering event, and derives an angle from the rendering time that goes from 0 to 2π every 4 seconds. The Math.Cos and Math.Sin methods implement the parametric equations for a circle by calculating values for the Canvas.Left and Canvas.Top attached properties:

namespace RevolutionNumber1
{
    public sealed partial class MainPage : Page
    {
        public MainPage()
        {
            this.InitializeComponent();
            CompositionTarget.Rendering += OnCompositionTargetRendering;
        }

        void OnCompositionTargetRendering(object sender, object args)
        {
            TimeSpan timespan = (args as RenderingEventArgs).RenderingTime;
            double fraction = ((double) timespan.Ticks /
                                    TimeSpan.FromSeconds(4).Ticks) % 1;
            double angle = fraction * 2 * Math.PI;
            Canvas.SetLeft(ellipse, 350 * Math.Cos(angle));
            Canvas.SetTop(ellipse, 350 * Math.Sin(angle));
        }
    }
}

Rather than host the ball in a Canvas, the Revolution No. 2 program defines a TranslateTransform on the ball so that it too can be moved around the screen:

Now the Ellipse has its own HorizontalAlignment and VerticalAlignment settings to position it in the center of the screen. The code-behind file is very similar to Revolution No. 1 except that it sets the X and Y properties of the TranslateTransform:

namespace RevolutionNumber2
{
    public sealed partial class MainPage : Page
    {
        public MainPage()
        {
            this.InitializeComponent();
            CompositionTarget.Rendering += OnCompositionTargetRendering;
        }

        void OnCompositionTargetRendering(object sender, object args)
        {
            TimeSpan timespan = (args as RenderingEventArgs).RenderingTime;
            double fraction = ((double)timespan.Ticks /
                                    TimeSpan.FromSeconds(4).Ticks) % 1;
            double angle = fraction * 2 * Math.PI;
            translate.X = 350 * Math.Cos(angle);
            translate.Y = 350 * Math.Sin(angle);
        }
    }
}

The other three solutions use XAML animations and don't involve the code-behind files.

Revolution No. 3 demonstrates the most conventional solution: a RotateTransform with a center of rotation in the center of the screen but the ball moved away from that center. To orient everything with the center of the ball, I constructed the ball from a Path using an EllipseGeometry with a center at (0, 0). Putting that Path in a Canvas shrunk down to the center of the screen also puts the ball in the center of the screen but allows the transforms to be relative to the ball's center rather than to the ball's upper-left corner.

This approach is different from all the others in that the ball itself actually rotates, even though you can't see it. The same half of the ball always faces the center of the screen, much like the Moon revolving around the Earth.

Is an all-XAML solution possible without a RotateTransform? I wouldn't have thought so until I started looking at the math behind the EasingFunctionBase derivatives. Basically, the animation easing functions use transfer functions to "bend time," which results in animations speeding up or slowing down. You might not think this speeding up and slowing down has anything to do with circular movement until you realize that a circle is simply horizontal and vertical movement that speeds up and slows down in reverse synchronization.

For example, let's look at SineEase (which I'm surprised isn't a trademark for a sinus medication). When the EasingMode property is set to the default value of EaseOut, this class defines a transfer function like so:

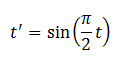
Like all the transfer functions, 0 goes to 0, 1 goes to 1, and the interesting stuff happens in between. By basing the transfer function on the first quarter of a sine curve, an animation starts fast and slows down.

You get the opposite effect with an EasingMode setting of EaseOut. The transfer function is a cosine curve but flipped around to go from 0 to 1:

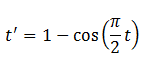
With an EasingMode setting of EaseInOut the transfer function is the first half of a cosine curve, again adjusted to go from 0 to 1:

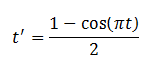
It starts slow, speeds up, and then slows down again. If you were to use the EaseInOut variation of SineEase with a DoubleAnimation applied to the Canvas.Left property of an Ellipse, and set AutoReverse equal to True and RepeatBehavior to Forever, you would get motion that resembles a pendulum: slow right before and after the motion reverses, but faster in the middle.

If you apply a similar animation to Canvas.Top but offset by half a cycle, you can move an object around in a circle, as the Revolution No. 4 program demonstrates:

Notice that the second animation has a BeginTime of 1 second, so for the first second after the program is loaded, the first animation moves the ellipse horizontally from –350 pixels to 0, and then the second animation kicks in and begins moving the ball vertically from –350 to 0 as the ball is moving horizontally from 0 to 350. Although the easing functions are intended to slow down and speed up animations, the ball actually has a constant angular velocity as it travels around in a circle.

I suspect the easing functions have driven the final nails into the coffin of the Spline_____KeyFrame classes, which can also slow down and speed up animations. These classes aren't nearly as easy to use as the easing functions because the transfer function is based on a Bézier spline curve and there are no prepackaged solutions. The Bézier curve always starts at (0, 0) and ends at (1, 1) but the two control points must be supplied by the programmer.

It occurred to me that a series of SplineDoubleKeyFrame objects could approximate quarter cycles of sine and cosine functions. To derive the appropriate spline curves, I wrote a little program with four nested for loops to try a bunch of values for the two control points and see which ones came closest. I found that control points of (0.3, 0.5) and (0.65, 1) approximate a sine curve fairly well, and the same control points flipped around approximate a cosine: (0.35, 0) and (0.7, 0.5).

And that's what's used in the Revolution No. 5 program:

I know it doesn't look like it, but this program also revolves the ball round the center of the screen. Source code is here.

Programming Windows, 6th Edition

Special Price through (approximately) July 2012!

For just $20, you get:

(1) the Consumer Preview ebook right now (with source code updated for the Release Preview)
(2) the Release Preview ebook in early August
(3) the final ebook in November

Programming Windows 6th Edition
Consumer Preview eBook