Charles Petzold

In the original 1988 edition of his book A Brief History of Time, Stephen Hawking famously revealed why the book contains virtually no mathematics:

Someone told me that each equation I included in the book would halve the sales. I therefore resolved not to have any equations at all. In the end, however, I did put in one equation, Einstein’s famous equation E = mc². I hope that this will not scare off half of my potential readers. (Acknowledgements, pgs. vi-vii)

I have come to think of this as Hawking’s Law of Diminishing Book Sales, and for books intended for a popular audience, I’m sure there is much truth in it. A potential reader leafing through the pages of A Brief History of Time while standing in a bookstore (the place where people purchased books in 1988) saw what appeared to be mostly nice friendly prose. “I can do this!”

In my free time I am working on a book entitled Computer of the Tides: Lord Kelvin’s Machine to Disprove Evolution and several months ago I posted a draft preview of Chapter 1. The book is a big-picture story of a tide-predicting machine now considered to be an early special-purpose analog computer, one of which is on display at the Science Museum in South Kensington, London.

In the 1860s and 1870s, Scottish scientist William Thomson (1824 – 1907), later known as Lord Kelvin, developed a harmonic theory of the tides based on Fourier analysis of data accumulated from tide gauges.

For the seaport from which the data is obtained, the tide-predicting machine is then programmed with the results and plots out the future rise and fall of the tides. As the crank is turned, the ten smaller wheels bob up and down in sinusoidal patterns. The frequency of each wheel’s rotation is governed by the gear ratios. Its amplitude and phase depend on the wheel’s offset from its center. A cable woven around these ten small wheels essentially sums them up, and the machine plots the function:

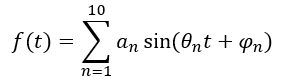
That function might make the machine clear and obvious to some people, but I am attempting to write this book with Hawking’s Law in mind, and if that equation appears at all in the book, it will be relegated to a technical appendix. What I prefer instead is for my readers to achieve an intuitive grasp of what the machine does without the explicit math.

The draft preview of Chapter 1 focuses on the Copernican Revolution and Isaac Newton in the context of the Glorious Revolution and the philosophy of John Locke. The closest I come to math in that chapter is the E = mc² of the 17th century: F = ma or force equals mass times acceleration.

Chapter 2 will present more challenges, however.

Chapter 2 must get the reader familiar with sine curves, and I hope to do this visually and intuitively without any scary mathematics. Although the sine curve originates in the study of triangles, it also describes many cyclical processes in the natural world, including the tides. I hope that Chapter 2 reveals why this is so.

Physicists know that sine curves frequently show up in the natural world because the sine function is the solution to the differential equation:

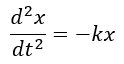
That equation represents a simple harmonic oscillator. But I certainly don’t want to delve into differential equations in the book, or even mention what they are! I need to tackle the equivalence in an intuitive way. The connection between the abstract mathematics of the triangle and the rhythms of the natural world is quite interesting to me from a perspective of the philosophy of mathematics, and I’d like to get that across in the chapter as well.

Attempting to make a book accessible to the math-phobic reader is a difficult balancing act. Obviously many of the potential readers of Computer of the Tides will be people interested in the history of science and technology. These readers are likely to be more comfortable with mathematics, and I don’t want to insult their intelligences. This implies that my discussion has to be fresh and original and different from any other book.

I originally intended for Chapter 2 to leap ahead a century and across the Channel to the French Revolution. The chapter would mostly focus on Joseph Fourier (1768 – 1830) but also touch upon an earlier generation of French savants, most prominently Pierre-Simon Laplace (1749 – 1827), known as “the French Newton.” Laplace made major strides in the physics of the tides. Fourier developed the concepts and mathematical tools that William Thomson drew upon for the harmonic theory of the tides.

Fourier also plays another role in the book: His major analytical work involved the propagation and dissipation of heat, and William Thomson was to use those analytical tools in determining how long the cooling Earth had been fit for the habitation of life.

For several months this year I was devoting my free weekends to a possible approach to introducing trigonometry and sine curves in the context of the writings of Laplace. But that discussion got much too long and complex. It just wasn’t working. It threw the whole rest of the chapter out of kilter. I could no longer work on it because I knew it was the wrong approach. The sine curve had to appear prior to Laplace’s entrance, as it did historically.

I realized that Laplace and Fourier had to be bumped to Chapter 3, and I had to conceive from scratch a whole new Chapter 2. This new Chapter 2 would form a bridge between the Glorious Revolution and the French Revolution, which fortunately is a very exciting period known as the Enlightenment. The sine curve could then be introduced in the context of the vibrating string controversy, which involved debates about the mathematical descriptions of the shape of a vibrating string. This attracted some of the most prominent mathematicians of the 18th century, two of whom also did research on the tides.

The vibrating string controversy is often approached historically in a purely physical and mathematical manner. But I wanted to put it into a more social context.

In the 18th century, vibrating strings were primarily found in harpsichords, which suggested that the subject could be approached through the music of the late Baroque, which includes not only the well-known composers such as Bach, Handel, and Vivaldi, but also Jean-Philippe Rameau. Besides composing harpsichord music and operas, Rameau wrote several ground-breaking books on harmony, and he also seems to have connections with all the prominent figures of the French Enlightenment: Voltaire wrote librettos for Rameau operas. Rousseau got into a public debate with Rameau over melody vs. harmony. Diderot wrote a book called “Rameau’s Nephew.” And because of his work on harmony, Rameau was known as “the Isaac Newton of Music.”

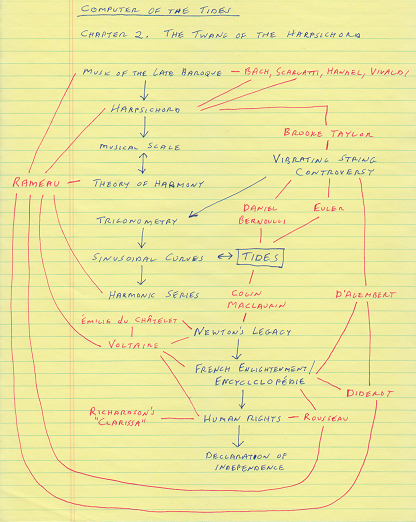
After some research, the various themes and interconnections of the new Chapter 2 fell into place fairly quickly. This afternoon I attempted to summarize the chapter on a single page of a yellow pad, and here it is:

Blue is for themes and topics; the major players are in red.

My goal in writing Chapter 2 is to get from the topic at the top of the page (Baroque music) to the topic at the bottom (the American Revolution) in an unbroken linear sequence of words, sentences, paragraphs, and illustrations.

And if this approach doesn’t work, I’ll try something else.